This page describes a finite element analysis of a bicycle wheel, something like a 700C touring wheel.
First of all, however: If at any time you think anything I present here assumes that a spoke withstands compression, read this.
And: If you think it's impossible to stand on something that's in tension, read this too.
And: If you think I'm claiming you can remove three quarters of
the spokes in a wheel, read this instead.
The purpose of this page is to consider a common question about bicycle type wheels: does the hub hang from the top spokes, or press on the lower spokes. Alternatively, does it do something in-between?.
If you really want to know about bicycle wheels, there's a book I'd recommend you read. It's called "The Bicycle Wheel", and it's by Jobst Brandt. It has about 150 pages about nothing but bicycle wheels. It covers theory and practice, how to analyse them and how to build them. One of the things the book includes is some finite element analysis of a typical bicycle wheel, to try and resolve this question.
This web page includes the results of the same exercise. Although I've done the exercise from scratch, the answers I get are qualitatively the same as those reported by Jobst Brandt. The numbers are slightly different, because of detail differences in the models, but they remain very close. The page goes on to examine some other wheel analyses (changing spoking patterns, cutting out spokes and so on).
But first, some semantics. It is traditional when debating the question of hanging or standing to define your terms to mean something other than what your opponent means. For example, define 'hang' as meaning 'have some tension force' and you can safely say that the hub hangs, because all the spokes have tension. The trouble with this definition is that it results in the conclusion that the hub hangs from something below it, which is not really compatible with the normal usage of the word.
In asking whether the hub hangs or stands on the spokes, I really mean to question where the structurally active spokes are. That is, if the spokes which resist load are below the hub, I'd describe the hub as standing on the lower spokes. If the spokes that resist load are above the hub, then I'd say the hub was hanging. That is:
By structurally active I mean the ones that are affected significantly by the load. That is, suppose you have some sort of table with four legs. Suppose it is standing on four weighing scales, one under each leg. You could put something on the table and see which scales changes most, i.e. which leg is contributing most to holding up the weight of that object. This would be the most structurally active leg. If I put a weight on the table-top, and one of the legs barely changed at all, I would not consider that that particular leg is holding up that weight (though it may be stabilising the table so other legs can support the weight).
Some people don't like these definitions. They feel that it can only be described as standing if compressive stress is involved. However, the most reliable dictionary definition I own ( The New Shorter Oxford English Dictionary, half a million definitions in two volumes each 1900 or so pages) makes no such restriction - the verb is the third entry for stand, and meaning 12 (the first within the second major grammatical division) is the relevant one - "Of a thing: be in an upright position with the lower part resting on or fixed in the ground or some other support". This is compatible with the definitions above - if the hub has its lower part supported by the spokes below it, from which the supporting action is predominately received, the definition fits. None of the meanings in the dictionary specify that compressive stress be involved. (Incidently, for the Americans, Merriam-Webster is the same - stand means "to rest or remain upright on a base or lower end", with no requirement for compressive stress.)
To make sense of what's coming up, you probably need to know why I've done some things (and not done others). To understand that, you need to understand some structural mechanics. This is probably first year degree course material, but the basic concepts are not too hard, and hopefully I can explain them well enough to make sense...
The first issue to address is that of linear superposition. What this means is that I'm not analysing all the stresses in the wheel. I know that all the spokes start out with a uniform tension, and I don't really care about it. For the purposes of the analysis I simply ignore it, and it goes away!
Therefore, when the analysis shows a force in a spoke, the real force in the spoke is whatever the preload (the initial tension) was, plus the force calculated. If the force was tension, we end up with a more highly stressed spoke. If the calculated load was compression we end up with a less tensile spoke. That is, a reference to a 'compressive' spoke could be read as a 'less tensile' spoke. To get the true state in the wheel you need to superimpose (ie, add) the results of this analysis on the initial state.
None of this affects the analysis. If we ignore buckling (or restrain against it), a spoke under tension which is subject to (say) 100N less tension contracts just as much as an unstressed spoke subject to 100N compression (or for that matter a compressive spoke subject to 100N more compression). In the analysis I simply don't tell the computer to let anything buckle, so I can analyse a spoke with compression without worrying that it's really a spoke that started out with a tension and now has less tension.
A wheel like this is statically indeterminate. For a statically indeterminate structure, the relative stiffness of the parts of the structure influences the loads in the parts. If you change the stiffness of one part, it changes the load in that part, and since the load has to come from (or go to) somewhere, consequently alters the loads in other parts of the structure. This means simple analogies like "imagine replacing all the spokes with elastic bands..." tend to fall down and reach the wrong conclusion, unless you also imagine replacing the rim with cooked spaghetti, and then you conclude that the wheel won't work at all!
To visualise the effect of statical indeterminacy, imagine a
flag-pole, with a horizontal force applied at the top. This is
a plain ordinary flag-pole with no guy-ropes or anything like that. Just
a pole, sticks straight up. This is statically determinate (opposite
of statically indeterminate) - you can
calculate the effects at the base without knowing anything about the
stiffness:
Suppose it's 6m high.
Suppose there's a horizontal force at the top of 1kN (N is a newton.
It's the SI unit of force. A newton is the force which accelerates 1kg at
1m/s2. 1kg weighs 9.81 newtons (roughly, at sea level, etc. etc.))
At the base, the bending moment will be 6kNm.
Now, imagine a second flag-pole alongside the first and the two are connected at the top by a rod. The rod freely pivots at each end. It can only conduct a pull or push. It is not unlike a bicycle spoke, though we are initially assuming it won't buckle (just to simplify matters). We've arranged the poles and rod so that they line up with the load applied.
Now I cannot calculate the bending moments at the base of either flagpole unless I know the bending stiffness of both poles and the axial stiffness of the rod.
For example:
When you get a statically indeterminate analysis to do, normally you turn to a computer. You can categorise analysis problems by the concept of degrees of freedom. These are (roughly) the number of different variables you need to solve. The flagpoles are a three degree of freedom problem, and I can solve any such problem with a pencil and paper (it becomes a set of simultaneous equations, or the inversion of a matrix). For much bigger problems, it's best to let the computer invert a matrix than do it by hand.
Finite element (FE) analysis is where you split a large complex problem up into small simple bits (the finite elements) that interact in simple ways. For example, it's difficult to write an equation that completely describes the behaviour of a wheel, but it's easy to do one that describes the behaviour of a spoke - a spoke has no bending and no shear, just axial load. Pull it and it stretches. Pull it twice as hard and it stretches twice as much.
Having split the problem into lots of finite elements you describe how the elements join together, then let the computer work out how they interact and come up with a solution. Easy in principal, sometimes a little more tricky in practice, because you can never model exactly what happens in the real world (the real world is too complicated), and you have to determine whether the simplifications you've made change the answers or not.
I actually generated the model file with a small program (a perl script) which wrote a command file to tell the FE program how to build the wheel. My script parametrises the problem, so I can easily generate models of (say) 28 spoke 1 cross 16 inch diameter wheels. The script and the method is described on the page about assembling the model.
As previously discussed, the stiffness of the components needs to be about right if we are to get answers that are about right. The dimensions therefore have to be about right because they affect the stiffness. An element with a given cross-section area subject to a given force will extend twice as far as one half the length, because the extension is a strain - which is a stretch-per-unit-of-original-length.
Thus, I must specify the dimensions, section properties and material properties I have adopted. This model isn't actually any particular wheel, but it's nearest to a 700C touring bike wheel with a box section alloy rim. There's a page where I discuss the model section properties in more detail, and compare the values with some other published analyses.
Geometry | The rim is a 600mm diameter circle. The hub ends of the spokes are on circles of 40mm diameter. This is a 3D model, and the two hub end circles are spaced 100mm apart (ie, 50mm either side of the plane of the rim). |
Spokes | The spokes are modelled as 2mm diameter axial load only members. They have a cross-sectional area of 3.14mm2. They are made material with a Young's modulus 205 000 N/mm2, which is a typical value for steel. |
Rim | The rim is a rectangular hollow box of external dims 25x10mm, side-walls 2mm thick, top and bottom faces 1mm thick. It has a cross-sectional area of 82 mm2, an I value in the plane of the wheel of 1187 mm4, and an I out of the plane of the wheel of 6847 mm4. These are curved beams without shear deformation, which I believe to be a reasonable simplification given their span:depth ratio. The material is generic aluminium alloy (E=75 000 N/mm2, poisson=0.3). |
Supports | The hub ends of all spokes have displacement restraint in x,
y and z. This makes it easier to see displacement of the rim, since it
eliminates the main effect which is a rigid body displacement downwards if I
restrain at the contact point and load at the hub.
The computer doesn't care if I hold the hub and load the rim, or hold the rim and load the hub. The answers are identical. Thus, it makes sense to restrain whichever makes it easiest to see the results. |
Loading | Loading is three upward point loads, 500N at very bottom of rim (centre of contact patch), 250N at each adjacent spoke/rim connection. This simulates quite a long contact patch. If the load is applied at a single node loads are concentrated on even fewer spokes. |
The only possibly significant simplification in this (I believe) is that the loading distribution is just a fudge which I guessed to be vaguely similar to the real situation for a touring type tyre. I've discussed this with someone who's actually measured some contact patches (loaded inked wheels on panes on glass and so on), who told me that my guess was pretty good. Unfortunately, I've lost the information, so if anyone knows of anything discussing this aspect, I'd be really pleased to hear about it.
In principle, I could do a better simulation of a tyre with some non-linear springs, but that would make the model a lot more complex, and raise issues of calibration (the distribution of stiffness between the springs would still be a guess by me) so I haven't done so yet.
Looks like this:

As you can see, it's 36 spokes, with a 3-cross pattern.
The first thing to do with a FE analysis results set is look at the deflected shape. Since you normally have tiny deflections, it is normal to exaggerate them. This is a deflected shape plot with the deflections multiplied 100 times. The maximum deflection was actually 0.1803 mm, but this plot shows a deflection of 18.03mm.
Generally it's easier to see what's happened if you superimpose the undeformed and the deformed mesh, so you can see what actually moved.
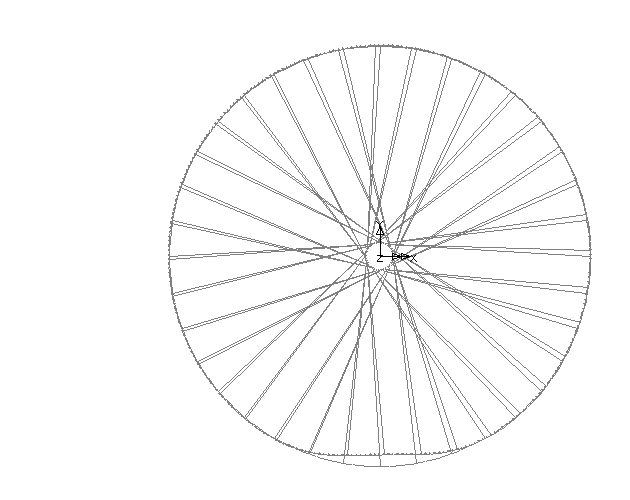
As you can see, what happened was that the rim deformed locally to the contact patch. You can see that almost all the spokes remain of the same length, and those near the load (ie, at the bottom of the wheel) shorten somewhat. This will have the effect of reducing the tension in those spokes. Remember that I put three points of load on. You can see that the deformation is very localised - the loaded spokes shorten, and one extra spoke each way shortens, but there's hardly any change further round the rim.
Next, of course, we look at the stresses in the components. Specifically, in this model we examine the forces in the spokes. here the spokes are coloured according to the change in force within them when 1000N (100kg, 220lbs) total load is applied. I've also labelled them with the actual value of tension (in N). Negative values indicate a compression. This is a change from the unloaded state, so compression doesn't actually mean compression, it means reduction in tension.
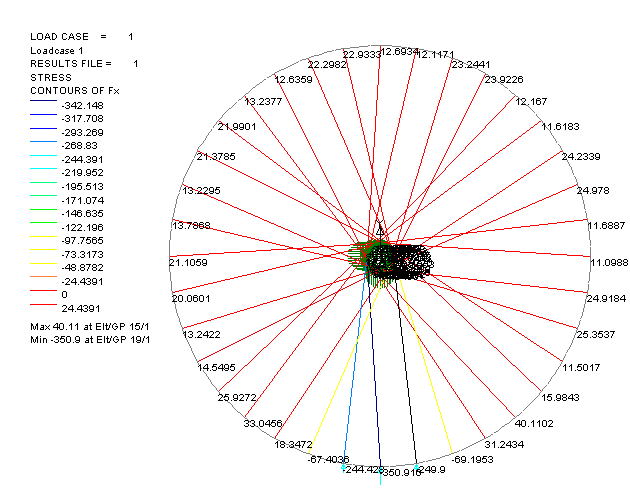
The plot is also available without the values, should you want it.
To examine these quantitatively, stick them in a spreadsheet:
| Element | Tension | in-plane angles | angle factors | vertical force | split by sign | split by location | ||||||||||||
| R | T | total | in plane | out plane | total | T | C | top | sides | bottom | ||||||||
| 1 | 12.693 | 0.00 | 3.42 | 3.42 | 0.9982 | 0.9855 | 0.9838 | 12.487 | 12.487 | 12.487 | ||||||||
| 2 | 12.117 | 10.00 | 3.42 | 13.42 | 0.9727 | 0.9855 | 0.9586 | 11.616 | 11.616 | 11.616 | ||||||||
| 3 | 23.244 | 20.00 | -3.42 | 16.58 | 0.9584 | 0.9855 | 0.9445 | 21.955 | 21.955 | 21.955 | ||||||||
| 4 | 23.923 | 30.00 | -3.42 | 26.58 | 0.8943 | 0.9855 | 0.8813 | 21.084 | 21.084 | 21.084 | ||||||||
| 5 | 12.167 | 40.00 | 3.42 | 43.42 | 0.7264 | 0.9855 | 0.7158 | 8.710 | 8.710 | 8.710 | ||||||||
| 6 | 11.618 | 50.00 | 3.42 | 53.42 | 0.5960 | 0.9855 | 0.5873 | 6.824 | 6.824 | 6.824 | ||||||||
| 7 | 24.234 | 60.00 | -3.42 | 56.58 | 0.5507 | 0.9855 | 0.5428 | 13.153 | 13.153 | 13.153 | ||||||||
| 8 | 24.978 | 70.00 | -3.42 | 66.58 | 0.3974 | 0.9855 | 0.3917 | 9.783 | 9.783 | 9.783 | ||||||||
| 9 | 11.689 | 80.00 | 3.42 | 83.42 | 0.1146 | 0.9855 | 0.1130 | 1.320 | 1.320 | 1.320 | ||||||||
| 10 | 11.099 | 90.00 | 3.42 | 93.42 | -0.0596 | 0.9855 | -0.0588 | -0.652 | -0.652 | -0.652 | ||||||||
| 11 | 24.918 | 100.00 | -3.42 | 96.58 | -0.1146 | 0.9855 | -0.1130 | -2.815 | -2.815 | -2.815 | ||||||||
| 12 | 25.354 | 110.00 | -3.42 | 106.58 | -0.2854 | 0.9855 | -0.2813 | -7.131 | -7.131 | -7.131 | ||||||||
| 13 | 11.502 | 120.00 | 3.42 | 123.42 | -0.5507 | 0.9855 | -0.5428 | -6.243 | -6.243 | -6.243 | ||||||||
| 14 | 15.984 | 130.00 | 3.42 | 133.42 | -0.6873 | 0.9855 | -0.6774 | -10.827 | -10.827 | -10.827 | ||||||||
| 15 | 40.110 | 140.00 | -3.42 | 136.58 | -0.7264 | 0.9855 | -0.7158 | -28.712 | -28.712 | -28.712 | ||||||||
| 16 | 31.243 | 150.00 | -3.42 | 146.58 | -0.8347 | 0.9855 | -0.8226 | -25.700 | -25.700 | -25.700 | ||||||||
| 17 | -69.195 | 160.00 | 3.42 | 163.42 | -0.9584 | 0.9855 | -0.9445 | 65.357 | 65.357 | 65.357 | ||||||||
| 18 | -249.900 | 170.00 | 3.42 | 173.42 | -0.9934 | 0.9855 | -0.9790 | 244.656 | 244.656 | 244.656 | ||||||||
| 19 | -350.916 | 180.00 | -3.42 | 176.58 | -0.9982 | 0.9855 | -0.9838 | 345.216 | 345.216 | 345.216 | ||||||||
| 20 | -244.428 | 190.00 | -3.42 | 186.58 | -0.9934 | 0.9855 | -0.9790 | 239.299 | 239.299 | 239.299 | ||||||||
| 21 | -67.404 | 200.00 | 3.42 | 203.42 | -0.9176 | 0.9855 | -0.9043 | 60.955 | 60.955 | 60.955 | ||||||||
| 22 | 18.347 | 210.00 | 3.42 | 213.42 | -0.8347 | 0.9855 | -0.8226 | -15.092 | -15.092 | -15.092 | ||||||||
| 23 | 33.046 | 220.00 | -3.42 | 216.58 | -0.8030 | 0.9855 | -0.7914 | -26.151 | -26.151 | -26.151 | ||||||||
| 24 | 25.927 | 230.00 | -3.42 | 226.58 | -0.6873 | 0.9855 | -0.6774 | -17.562 | -17.562 | -17.562 | ||||||||
| 25 | 14.550 | 240.00 | 3.42 | 243.42 | -0.4475 | 0.9855 | -0.4410 | -6.416 | -6.416 | -6.416 | ||||||||
| 26 | 13.242 | 250.00 | 3.42 | 253.42 | -0.2854 | 0.9855 | -0.2813 | -3.724 | -3.724 | -3.724 | ||||||||
| 27 | 20.060 | 260.00 | -3.42 | 256.58 | -0.2321 | 0.9855 | -0.2287 | -4.588 | -4.588 | -4.588 | ||||||||
| 28 | 21.106 | 270.00 | -3.42 | 266.58 | -0.0596 | 0.9855 | -0.0588 | -1.240 | -1.240 | -1.240 | ||||||||
| 29 | 13.787 | 280.00 | 3.42 | 283.42 | 0.2321 | 0.9855 | 0.2287 | 3.153 | 3.153 | 3.153 | ||||||||
| 30 | 13.230 | 290.00 | 3.42 | 293.42 | 0.3974 | 0.9855 | 0.3917 | 5.182 | 5.182 | 5.182 | ||||||||
| 31 | 21.379 | 300.00 | -3.42 | 296.58 | 0.4475 | 0.9855 | 0.4410 | 9.428 | 9.428 | 9.428 | ||||||||
| 32 | 21.990 | 310.00 | -3.42 | 306.58 | 0.5960 | 0.9855 | 0.5873 | 12.916 | 12.916 | 12.916 | ||||||||
| 33 | 13.238 | 320.00 | 3.42 | 323.42 | 0.8030 | 0.9855 | 0.7914 | 10.476 | 10.476 | 10.476 | ||||||||
| 34 | 12.636 | 330.00 | 3.42 | 333.42 | 0.8943 | 0.9855 | 0.8813 | 11.136 | 11.136 | 11.136 | ||||||||
| 35 | 22.298 | 340.00 | -3.42 | 336.58 | 0.9176 | 0.9855 | 0.9043 | 20.165 | 20.165 | 20.165 | ||||||||
| 36 | 22.933 | 350.00 | -3.42 | 346.58 | 0.9727 | 0.9855 | 0.9586 | 21.984 | 21.984 | 21.984 | ||||||||
| === | === | === | === | === | === | |||||||||||||
| 1000.000 | 44.518 | 955.483 | 139.612 | 0.561 | 859.827 | |||||||||||||
| average split T / C: | 1.436 | 191.097 | ||||||||||||||||
Spoke number starts counting at top dead centre of the rim and works round clockwise. R and T are the radial and tangential components of the spoking pattern, summated to give a total angle, which is degrees clockwise from vertical. The angle factors are to split out the vertical component of spoke tension. They are the cosine of the spoke in plane total angle, and the cosine of the angle between the spoke and the plane of the rim. Total is the product of in plane and out of plane.
The tension is taken from the analysis. Multiplying the axial force by the total angle factor gives the vertical component of the force. This is the lift that one particular spoke is contributing to the hub. If we add them up, we should get 1000, and luckily we do.
Then, I've split the lift forces into two columns, depending upon whether the spoke force was tensile or compressive. This is to see if the hub hangs from tensile spokes, or stands on compressive ones.
Put it another way - the average compressive spoke contributes 133 times as much lift force as the average tensile spoke.
Finally I've split the figures by location - which quarter of the rim the spoke attaches to.
All sorts of other interesting observations emerge.
From these figures, I conclude that it is perfectly reasonable to say that the hub stands on the lower spokes, and that it does not hang from the upper spokes.
It is also wrong to say that the force distributes all around the rim and all the spokes contribute to holding up the hub - over a third of the spokes have an effect that pulls the hub down!
So, I've resolved the question (to my satisfaction, anyway) of standing or hanging. Now I've got an analysis model, it's interesting to see what else I can find out:
There's lots more that could be done, but to be honest, I'm not going to get round to this in teh foreseeable future:
back to www.astounding.org.uk top contents
page
To comment on anything (please do) email ian@astounding.org.uk